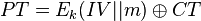| As of August 2020 the site you are on (wiki.newae.com) is deprecated, and content is now at rtfm.newae.com. |
Difference between revisions of "AES-CCM Attack"
(Tag: VisualEditor) |
|||
| Line 1: | Line 1: | ||
| + | WARNING: This page under construction! | ||
| + | |||
The following is an overview of the AES-CMM attack done by Eyal Ronen, detailed in his paper [http://iotworm.eyalro.net/ IoT Goes Nuclear: Creating a ZigBee Chain Reaction]. If using this attack please '''do not cite this page''', instead cite the original research. Note as of now (Nov/2016) the paper has not been submitted to any conference, so this is still very much new/draft research. | The following is an overview of the AES-CMM attack done by Eyal Ronen, detailed in his paper [http://iotworm.eyalro.net/ IoT Goes Nuclear: Creating a ZigBee Chain Reaction]. If using this attack please '''do not cite this page''', instead cite the original research. Note as of now (Nov/2016) the paper has not been submitted to any conference, so this is still very much new/draft research. | ||
| + | |||
| + | This page is presented as an example of using Python/ChipWhisperer to perform attacks against the AES-CCM cipher, without needing to do a more complex attack against AES-CTR mode. | ||
== AES-CCM Overview == | == AES-CCM Overview == | ||
| + | |||
| + | AES-CCM provides both encryption and authentication using the AES block cipher. This is a widely used mode since it requires only a single cryptographic primitive. That primitive is used in two different modes: CBC and CTR mode. The difference is explained below: | ||
| + | |||
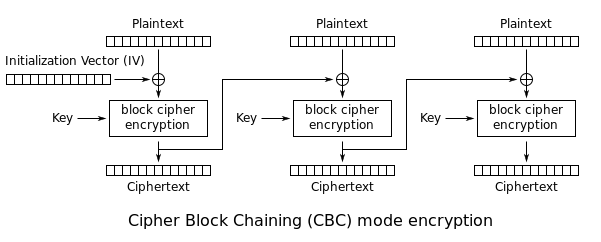
| + | '''Cipher Block Chaining (CBC):''' The plaintext is XORed with the previous ciphertext before being encrypted. There is no ciphertext before the first plaintext, so a randomly chosen initialization vector (IV) is used instead: | ||
| + | |||
| + | [[File:Block-Cipher-CBC.png]] | ||
| + | |||
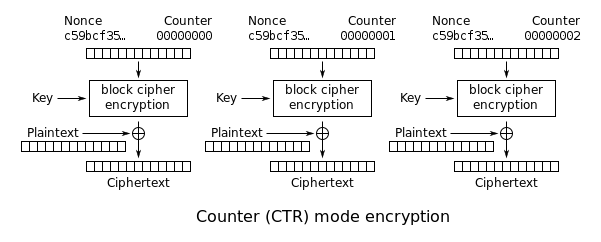
| + | '''Counter (CTR):''' An incrementing counter is encrypted to produce a sequence of blocks, which are XORed with the plaintexts to produce the ciphertexts: | ||
| + | |||
| + | [[File:Block-Cipher-CTR.png]] | ||
| + | |||
== Background on Attack == | == Background on Attack == | ||
| + | |||
| + | The following uses the notation from [http://iotworm.eyalro.net/ IoT Goes Nuclear: Creating a ZigBee Chain Reaction]. | ||
| + | |||
| + | Assume first the basic AES-ECB cipher is $CT = E_k(PT)$, where we are encrypting a block with secret key $k$. | ||
| + | |||
| + | AES-CCM combines AES-CTR mode and AES-CBC mode as mentioned. We could consider AES-CTR to be performing the following operation: | ||
| + | |||
| + | <math> | ||
| + | PT = E_k({IV || m}) \oplus CT | ||
| + | </math> | ||
| + | |||
== Performing Attack == | == Performing Attack == | ||
Revision as of 09:13, 2 November 2016
WARNING: This page under construction!
The following is an overview of the AES-CMM attack done by Eyal Ronen, detailed in his paper IoT Goes Nuclear: Creating a ZigBee Chain Reaction. If using this attack please do not cite this page, instead cite the original research. Note as of now (Nov/2016) the paper has not been submitted to any conference, so this is still very much new/draft research.
This page is presented as an example of using Python/ChipWhisperer to perform attacks against the AES-CCM cipher, without needing to do a more complex attack against AES-CTR mode.
Contents
AES-CCM Overview
AES-CCM provides both encryption and authentication using the AES block cipher. This is a widely used mode since it requires only a single cryptographic primitive. That primitive is used in two different modes: CBC and CTR mode. The difference is explained below:
Cipher Block Chaining (CBC): The plaintext is XORed with the previous ciphertext before being encrypted. There is no ciphertext before the first plaintext, so a randomly chosen initialization vector (IV) is used instead:
Counter (CTR): An incrementing counter is encrypted to produce a sequence of blocks, which are XORed with the plaintexts to produce the ciphertexts:
Background on Attack
The following uses the notation from IoT Goes Nuclear: Creating a ZigBee Chain Reaction.
Assume first the basic AES-ECB cipher is $CT = E_k(PT)$, where we are encrypting a block with secret key $k$.
AES-CCM combines AES-CTR mode and AES-CBC mode as mentioned. We could consider AES-CTR to be performing the following operation: