As of August 2020 the site you are on (wiki.newae.com) is deprecated, and content is now at rtfm.newae.com.

Difference between revisions of "AES-CCM Attack"

From ChipWhisperer Wiki
Jump to: navigation, search
(→‎Background on Attack)
(→‎Step #1: AES-CBC MAC Block #1)
Line 44: Line 44:
 
<TODO>
 
<TODO>
  
−
I've gone out of my way & marked the location of AES on it. Let's assume you didn't have that - why might you do? We can actually first do a CPA attack with the "XOR" leakage model:
+
I've gone out of my way & marked the location of AES on it. Let's assume you didn't have that - why might you do? We can actually first do a CPA attack with the "XOR" leakage model to determine where data is being manipulated.
 +
 
 +
==== 1-B: Finding interesting areas ====
 +
 
 +
Doing this requires switching the attack algorithm to the '''AddRoundKey''' output (where AddRoundKey is just an XOR operation):
  
 
<TODO>
 
<TODO>
Line 63: Line 67:
 
* AddRoundKey of previous during AES-ECB block.
 
* AddRoundKey of previous during AES-ECB block.
  
 +
==== 1-C: Modified First-Round Key ====
 +
 +
The first step is to perform a standard CPA attack. The only issue is we won't recover the actual encryption key used <math>k</math>, instead we recover <math>k \oplus CBC_{m-1} \oplus CTR_{m}</math>, since we basically roll all the constant inputs into what we call a `modified key'.
 +
 +
So let's do a first-round attack focused around points (180000,22000) to start (roughly picked from the power traces). To do this:
 +
* Turn back on all bytes (if previously disabled).
 +
* Switch leakage model to S-Box output.
 +
 +
You'll likely find after a number of traces you could plot correlation for bytes 0 & 15, and get a better idea where the attack should happen. Looking at the following I can see we could focus on points (18600,19200) and might get a more reliable attack.
 +
 +
Finally, you should get this `modified key', in this example we can see it appears to be '''94 28 5D 4D 6D CF EC 08 D8 AC DD F6 BE 25 A4 99''':
 +
 +
(block1_round1_key.png)
 +
 +
The next step is to use this to recover the complete round-key.
 +
 +
==== 1-D: True Second-Round Key ====
 +
 +
In what might seem like magic, we can use this modified key to directly determine the second-round key (the true key). This was originally presented by J. Jaffe in [https://www.iacr.org/archive/ches2007/47270001/47270001.pdf A First-Order DPA Attack Against AES in Counter Mode with Unknown Initial Counter]. The reason this works is if you remember we recovered  <math>k' = k \oplus CBC_{m-1} \oplus CTR_{m}</math>. In the AES algorithm the first thing we do is the AddRoundKey, which is:
 +
 +
<math>AddRoundKey(a,b) = a \oplus b</math>.
 +
 +
In the true algorithm we have the case of:
 +
<math>AddRoundKey(k, CBC_{m-1} \oplus CTR_{m} \oplus CT)</math>
 +
 +
And when we use our modified key, we are feeding the CT directly into AddRoundKey:
 +
<math>AddRoundKey(k', CT)</math>
  
−
180000 - 22000. We can now bring that down to (18600,19200)
+
Where the <math>k'</math> basically includes those additional constants, instead of them being added as part of the ciphertext. Ultimately it means the output of AddRoundKey, and thus processing of later rounds, is identical in both cases. So we can perform a CPA attack on the 2nd-round key, and directly recover the "true" first-round key by rolling back the key schedule.
  
 
=== Step #2: AES-CBC MAC Block #2 ===
 
=== Step #2: AES-CBC MAC Block #2 ===

Revision as of 19:50, 2 November 2016

WARNING: This page under construction!

The following is an overview of the AES-CMM attack done by Eyal Ronen, detailed in his draft/limited release paper IoT Goes Nuclear: Creating a ZigBee Chain Reaction. If using this attack please do not cite this page, instead cite the research paper only. The paper is currently a draft so there is no proceedings information etc as it has not yet been presented anywhere.

This page is presented as an example of using Python/ChipWhisperer to perform attacks against the AES-CCM cipher, without needing to do a more complex attack against AES-CTR mode.

AES-CCM Overview

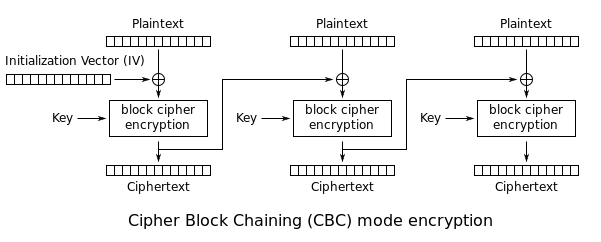
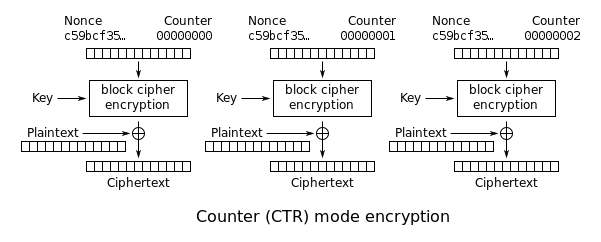
AES-CCM provides both encryption and authentication using the AES block cipher. This is a widely used mode since it requires only a single cryptographic primitive. That primitive is used in two different modes: CBC and CTR mode. The difference is explained below:

Cipher Block Chaining (CBC): The plaintext is XORed with the previous ciphertext before being encrypted. There is no ciphertext before the first plaintext, so a randomly chosen initialization vector (IV) is used instead:

Block-Cipher-CBC.png

Counter (CTR): An incrementing counter is encrypted to produce a sequence of blocks, which are XORed with the plaintexts to produce the ciphertexts:

Block-Cipher-CTR.png


Background on Attack

The following uses the notation from IoT Goes Nuclear: Creating a ZigBee Chain Reaction.

Assume first the basic AES-ECB cipher is 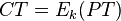CT = E_k(PT), where we are encrypting a block with secret key k.

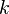AES-CCM combines AES-CTR mode and AES-CBC mode as mentioned. We could consider AES-CTR to be performing the following operation:

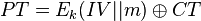
PT = E_k({IV || m}) \oplus CT

The problem with a straight-forward CPA attack on CTR mode is only 2 bytes vary (the number of bytes with 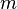m), so the CPA attack cannot recover all bytes of the key. A solution to this is presented in the paper

Performing Attack

Building Example

Collecting Traces

Step #1: AES-CBC MAC Block #1

The first step is to recover the AES encryption key used in round 1. This isn't too difficult - we'll first take our power traces, which if you recall look something like this:

<TODO>

I've gone out of my way & marked the location of AES on it. Let's assume you didn't have that - why might you do? We can actually first do a CPA attack with the "XOR" leakage model to determine where data is being manipulated.

1-B: Finding interesting areas

Doing this requires switching the attack algorithm to the AddRoundKey output (where AddRoundKey is just an XOR operation):

<TODO>

Note running it against all points might give you a memory error (especially on a 32-bit system). We don't need all bytes though, so to avoid this just change these settings:

  • Only enable a single subkey (i.e., say byte 0).
  • Set reporting interval & traces per attack to same value (say 100 I used here).

The result will show you correlation where the input data was used (possibly XORd with any constant). You'll get something like the top graph, where I've added an overlay of the power trace below it:

<TODO>

Note this is basically showing us where the AES-CTR output occurs, then where the AES-CBC input happens. The correlations correspond to the following I think (there may be a mixup of where the load occurs - if any of those intermediate states are loaded/saved it would show up):

  • Load of CT data.
  • XOR of AES-CTR output 'pad' with input CT.
  • XOR of previous with the old AES-CBC state as part of AES-CBC input processing.
  • AddRoundKey of previous during AES-ECB block.

1-C: Modified First-Round Key

The first step is to perform a standard CPA attack. The only issue is we won't recover the actual encryption key used 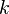k, instead we recover 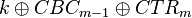k \oplus CBC_{m-1} \oplus CTR_{m}, since we basically roll all the constant inputs into what we call a `modified key'.

So let's do a first-round attack focused around points (180000,22000) to start (roughly picked from the power traces). To do this:

  • Turn back on all bytes (if previously disabled).
  • Switch leakage model to S-Box output.

You'll likely find after a number of traces you could plot correlation for bytes 0 & 15, and get a better idea where the attack should happen. Looking at the following I can see we could focus on points (18600,19200) and might get a more reliable attack.

Finally, you should get this `modified key', in this example we can see it appears to be 94 28 5D 4D 6D CF EC 08 D8 AC DD F6 BE 25 A4 99:

(block1_round1_key.png)

The next step is to use this to recover the complete round-key.

1-D: True Second-Round Key

In what might seem like magic, we can use this modified key to directly determine the second-round key (the true key). This was originally presented by J. Jaffe in A First-Order DPA Attack Against AES in Counter Mode with Unknown Initial Counter. The reason this works is if you remember we recovered 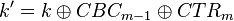k' = k \oplus CBC_{m-1} \oplus CTR_{m}. In the AES algorithm the first thing we do is the AddRoundKey, which is:

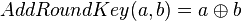AddRoundKey(a,b) = a \oplus b.

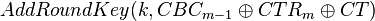
In the true algorithm we have the case of: AddRoundKey(k, CBC_{m-1} \oplus CTR_{m} \oplus CT)

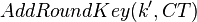
And when we use our modified key, we are feeding the CT directly into AddRoundKey: AddRoundKey(k', CT)

Where the 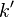k' basically includes those additional constants, instead of them being added as part of the ciphertext. Ultimately it means the output of AddRoundKey, and thus processing of later rounds, is identical in both cases. So we can perform a CPA attack on the 2nd-round key, and directly recover the "true" first-round key by rolling back the key schedule.

Step #2: AES-CBC MAC Block #2

Step #3: Recovery of AES-CTR Nonce

Step #4: Recovery of AES-CBC I.V.

Step #5: AES-CTR Pad

Example Bootloader

The example bootloader has a simplified AES-CCM implementation (NB: do NOT use this as a reference for a good implementation!). It accomplishes the basic goals only of having:

  • Header data that is authenticated but not encrypted
  • An encrypted MAC tag
  • A bunch of encrypted firmware blocks

Each block sent to the bootloader is 19 bytes long. The first byte indicates the type - header, auth tag, or data. If a new 'header' message is received it will abort any ongoing processing of existing data and restart the bootloader process.

All messages share this feature:

  • CRC-16: A 16-bit checksum using the CRC-CCITT polynomial (0x1021). The LSB of the CRC is sent first, followed by the MSB. The bootloader will reply over the serial port, describing whether or not this CRC check was valid.

Header Frame

  • 0x01: 1 byte of fixed header
  • Header Info: 14 bytes of "header" data which could be version or other such stuff.
  • Length: Number of encrypted data frames (NOT including the auth-tag frame) that will follow.

Note the 16 bytes of the header info + length are fed into the AES-CBC algorithm as part of the auth-tag generation. That is this data is authenticated but not encrypted. 

+------+------+------+------+ .... +------+------+------+------+
| 0x01 |     Header Info (14 bytes)|    Length   |   CRC-16    |
+------+------+------+------+ .... +------+------+------+------+

Auth Tag Frame

  • 0x02: 1 byte of fixed header
  • Auth-Tag: The expected output of the AES-CBC algorithm after processing the authenticated only data + decrypted data frames. This is then encrypted in AES-CTR mode with the CTR set to 0.
       
       |<----- Encrypted block (16 bytes) ------>|
       |    AES-CTR Encryption with CTR=0        |
       |                                         |
+------+------+------+------+ .... +------+------+------+------+
| 0x02 |     Auth-Tag (encrypted MAC)            |   CRC-16    |
+------+------+------+------+ .... +------+------+------+------+

Data block frame

  • 0x03: 1 byte of fixed header
  • Encrypted Data: Data encrypted in AES-CTR mode, with the CTR starting at 1 and incrementing.
       |<----- Encrypted block (16 bytes) ------>|
       |   AES-CTR Encryption with CTR=1,2,3..N  |
       |                                         |
+------+------+------+------+ .... +------+------+------+------+
| 0x03 |            Data (16 Bytes)              |   CRC-16    |
+------+------+------+------+ .... +------+------+------+------+


The bootloader responds to each command with a single byte indicating if the CRC-16 was OK or not: 

            +------+
CRC-OK:     | 0xA1 |
            +------+

            +------+
CRC Failed: | 0xA4 |
            +------+

Once ALL messages are received, the bootloader will respond with a signature OK or not message: 

            +------+
Sig-OK:     | 0xB1 |
            +------+

            +------+
Sig Failed: | 0xB4 |
            +------+

Note details of the AES-CTR nonce, AES-CBC I.V., and key are stored in the firmware itself. In this example they are not downloaded as part of the encrypted firmware file.

Retrieved from "http://wiki.newae.com/index.php?title=AES-CCM_Attack&oldid=1404"