| As of August 2020 the site you are on (wiki.newae.com) is deprecated, and content is now at rtfm.newae.com. |
Difference between revisions of "AES-CCM Attack"
(→Performing Attack) |
(→Step #1: AES-CBC MAC Block #1) |
||
| Line 42: | Line 42: | ||
The first step is to recover the AES encryption key used in round 1. This isn't too difficult - we'll first take our power traces, which if you recall look something like this: | The first step is to recover the AES encryption key used in round 1. This isn't too difficult - we'll first take our power traces, which if you recall look something like this: | ||
| − | [[File:powertrace_aesccm_block1.png| | + | [[File:powertrace_aesccm_block1.png|800px]] |
I've gone out of my way & marked the location of AES on it. Let's assume you didn't have that - why might you do? We can actually first do a CPA attack with the "XOR" leakage model to determine where data is being manipulated. | I've gone out of my way & marked the location of AES on it. Let's assume you didn't have that - why might you do? We can actually first do a CPA attack with the "XOR" leakage model to determine where data is being manipulated. | ||
| Line 50: | Line 50: | ||
Doing this requires switching the attack algorithm to the '''AddRoundKey''' output (where AddRoundKey is just an XOR operation): | Doing this requires switching the attack algorithm to the '''AddRoundKey''' output (where AddRoundKey is just an XOR operation): | ||
| − | [[File:roundkey_cpa_select.png| | + | [[File:roundkey_cpa_select.png|300px]] |
Note running it against all points might give you a memory error (especially on a 32-bit system). We don't need all bytes though, so to avoid this just change these settings: | Note running it against all points might give you a memory error (especially on a 32-bit system). We don't need all bytes though, so to avoid this just change these settings: | ||
| Line 59: | Line 59: | ||
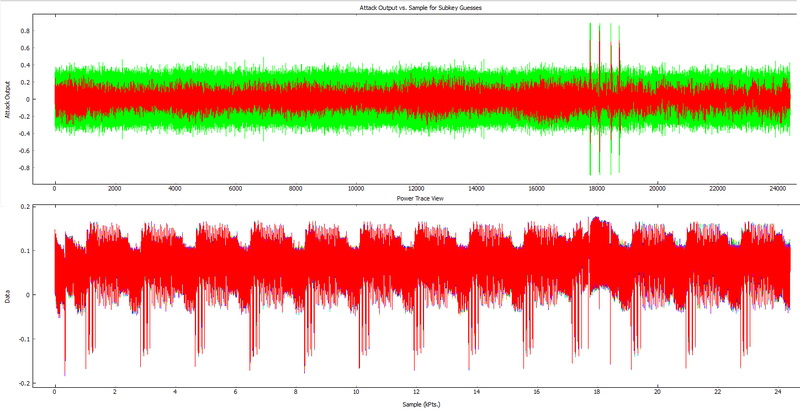
The result will show you correlation where the input data was used (possibly XORd with any constant). You'll get something like the top graph, where I've added an overlay of the power trace below it: | The result will show you correlation where the input data was used (possibly XORd with any constant). You'll get something like the top graph, where I've added an overlay of the power trace below it: | ||
| − | [[File:xor_comparison_powertrace.png| | + | [[File:xor_comparison_powertrace.png|800px]] |
Note this is basically showing us where the AES-CTR output occurs, then where the AES-CBC input happens. The correlations correspond to the following I think (there may be a mixup of where the load occurs - if any of those intermediate states are loaded/saved it would show up): | Note this is basically showing us where the AES-CTR output occurs, then where the AES-CBC input happens. The correlations correspond to the following I think (there may be a mixup of where the load occurs - if any of those intermediate states are loaded/saved it would show up): | ||
| Line 79: | Line 79: | ||
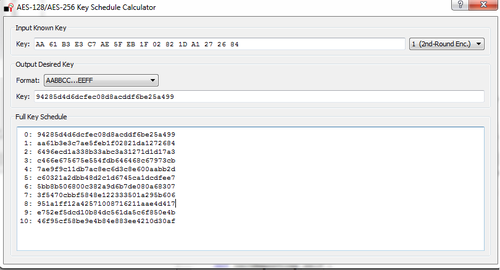
Finally, you should get this `modified key', in this example we can see it appears to be '''94 28 5D 4D 6D CF EC 08 D8 AC DD F6 BE 25 A4 99''': | Finally, you should get this `modified key', in this example we can see it appears to be '''94 28 5D 4D 6D CF EC 08 D8 AC DD F6 BE 25 A4 99''': | ||
| − | [[File:block1_round1_key.png| | + | [[File:block1_round1_key.png|800px]] |
The next step is to use this to recover the complete round-key. | The next step is to use this to recover the complete round-key. | ||
| Line 120: | Line 120: | ||
You can perform the same CPA attack, modified to occur around the second round. In this example I found points (20520, 21950) worked well - but you can try a much larger point-range, and then scale that down to get a faster calculation. This gives us the round-2 key, in this example appears to be '''AA 61 B3 E3 C7 AE 5F EB 1F 02 82 1D A1 27 26 84''': | You can perform the same CPA attack, modified to occur around the second round. In this example I found points (20520, 21950) worked well - but you can try a much larger point-range, and then scale that down to get a faster calculation. This gives us the round-2 key, in this example appears to be '''AA 61 B3 E3 C7 AE 5F EB 1F 02 82 1D A1 27 26 84''': | ||
| − | [[File:block1_round2_key.png| | + | [[File:block1_round2_key.png|800px]] |
Using the key-schedule widget, you can then determine the true initial key was '''94285d4d6dcfec08d8acddf6be25a499''' (which matches what was programmed in this example): | Using the key-schedule widget, you can then determine the true initial key was '''94285d4d6dcfec08d8acddf6be25a499''' (which matches what was programmed in this example): | ||
| − | [[File:keyschedule.png| | + | [[File:keyschedule.png|500px]] |
Note in addition you can perform the operation <math>k' \oplus k</math> to recover <math>CBC_{m-1} \oplus CTR_{m}</math>. If we knew either one of those we could then completely break AES-CCM, since we would know the AES-CBC I.V., along with the AES-CTR nonce/format. | Note in addition you can perform the operation <math>k' \oplus k</math> to recover <math>CBC_{m-1} \oplus CTR_{m}</math>. If we knew either one of those we could then completely break AES-CCM, since we would know the AES-CBC I.V., along with the AES-CTR nonce/format. | ||
Revision as of 20:22, 2 November 2016
WARNING: This page under construction!
The following is an overview of the AES-CMM attack done by Eyal Ronen, detailed in his draft/limited release paper IoT Goes Nuclear: Creating a ZigBee Chain Reaction. If using this attack please do not cite this page, instead cite the research paper only. The paper is currently a draft so there is no proceedings information etc as it has not yet been presented anywhere.
This page is presented as an example of using Python/ChipWhisperer to perform attacks against the AES-CCM cipher, without needing to do a more complex attack against AES-CTR mode.
Contents
AES-CCM Overview
AES-CCM provides both encryption and authentication using the AES block cipher. This is a widely used mode since it requires only a single cryptographic primitive. That primitive is used in two different modes: CBC and CTR mode. The difference is explained below:
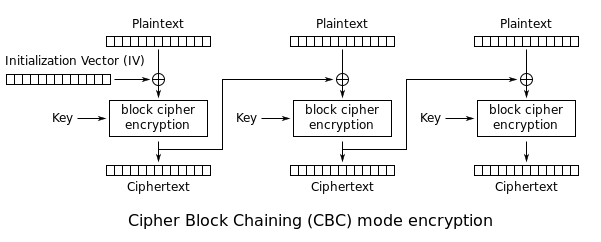
Cipher Block Chaining (CBC): The plaintext is XORed with the previous ciphertext before being encrypted. There is no ciphertext before the first plaintext, so a randomly chosen initialization vector (IV) is used instead:
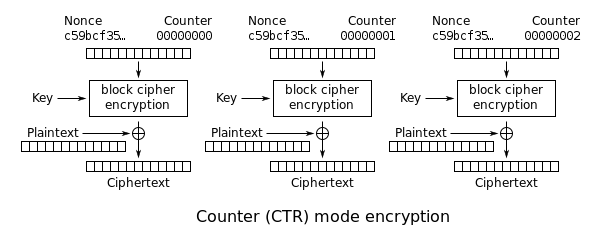
Counter (CTR): An incrementing counter is encrypted to produce a sequence of blocks, which are XORed with the plaintexts to produce the ciphertexts:
Background on Attack
The following uses the notation from IoT Goes Nuclear: Creating a ZigBee Chain Reaction.
Assume first the basic AES-ECB cipher is 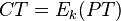 , where we are encrypting a block with secret key
, where we are encrypting a block with secret key 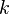 .
.
AES-CCM combines AES-CTR mode and AES-CBC mode as mentioned. We could consider AES-CTR to be performing the following operation:
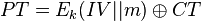
The problem with a straight-forward CPA attack on CTR mode is only 2 bytes vary (the number of bytes with 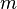 ), so the CPA attack cannot recover all bytes of the key. A solution to this is presented in the paper
), so the CPA attack cannot recover all bytes of the key. A solution to this is presented in the paper
Performing Attack
Building Example
Collecting Traces
Step #1: AES-CBC MAC Block #1
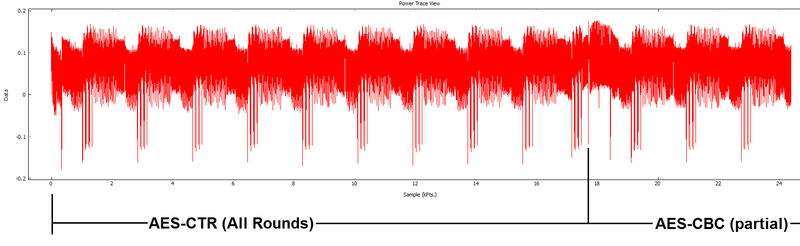
The first step is to recover the AES encryption key used in round 1. This isn't too difficult - we'll first take our power traces, which if you recall look something like this:
I've gone out of my way & marked the location of AES on it. Let's assume you didn't have that - why might you do? We can actually first do a CPA attack with the "XOR" leakage model to determine where data is being manipulated.
1-B: Finding interesting areas
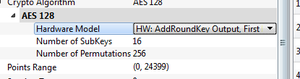
Doing this requires switching the attack algorithm to the AddRoundKey output (where AddRoundKey is just an XOR operation):
Note running it against all points might give you a memory error (especially on a 32-bit system). We don't need all bytes though, so to avoid this just change these settings:
- Only enable a single subkey (i.e., say byte 0).
- Set reporting interval & traces per attack to same value (say 100 I used here).
The result will show you correlation where the input data was used (possibly XORd with any constant). You'll get something like the top graph, where I've added an overlay of the power trace below it:
Note this is basically showing us where the AES-CTR output occurs, then where the AES-CBC input happens. The correlations correspond to the following I think (there may be a mixup of where the load occurs - if any of those intermediate states are loaded/saved it would show up):
- Load of CT data.
- XOR of AES-CTR output 'pad' with input CT.
- XOR of previous with the old AES-CBC state as part of AES-CBC input processing.
- AddRoundKey of previous during AES-ECB block.
1-C: Modified First-Round Key
The first step is to perform a standard CPA attack. The only issue is we won't recover the actual encryption key used 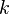 , instead we recover
, instead we recover 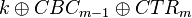 , since we basically roll all the constant inputs into what we call a `modified key'.
, since we basically roll all the constant inputs into what we call a `modified key'.
So let's do a first-round attack focused around points (180000,22000) to start (roughly picked from the power traces). To do this:
- Turn back on all bytes (if previously disabled).
- Switch leakage model to S-Box output.
You'll likely find after a number of traces you could plot correlation for bytes 0 & 15, and get a better idea where the attack should happen. Looking at the following I can see we could focus on points (18600,19200) and might get a more reliable attack.
Finally, you should get this `modified key', in this example we can see it appears to be 94 28 5D 4D 6D CF EC 08 D8 AC DD F6 BE 25 A4 99:
The next step is to use this to recover the complete round-key.
1-D: True Second-Round Key
In what might seem like magic, we can use this modified key to directly determine the second-round key (the true key). This was originally presented by J. Jaffe in A First-Order DPA Attack Against AES in Counter Mode with Unknown Initial Counter. The reason this works is if you remember we recovered 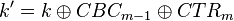 . In the AES algorithm the first thing we do is the AddRoundKey, which is:
. In the AES algorithm the first thing we do is the AddRoundKey, which is:
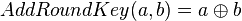 .
.
In the true algorithm we have the case of:
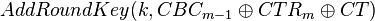
And when we use our modified key, we are feeding the CT directly into AddRoundKey:
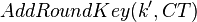
Where the 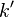 basically includes those additional constants, instead of them being added as part of the ciphertext. Ultimately it means the output of AddRoundKey, and thus processing of later rounds, is identical in both cases. So we can perform a CPA attack on the 2nd-round key, and directly recover the "true" first-round key by rolling back the key schedule.
basically includes those additional constants, instead of them being added as part of the ciphertext. Ultimately it means the output of AddRoundKey, and thus processing of later rounds, is identical in both cases. So we can perform a CPA attack on the 2nd-round key, and directly recover the "true" first-round key by rolling back the key schedule.
This requires a custom leakage model, which we can make fairly easily:
from chipwhisperer.analyzer.attacks.models.AES128_8bit import AESLeakageHelper
class Round2(AESLeakageHelper):
name = 'HW: Round-2 Key'
def leakage(self, pt, ct, key, bnum):
r1key = [0x94, 0x28, 0x5D, 0x4D, 0x6D, 0xCF, 0xEC, 0x08, 0xD8, 0xAC, 0xDD, 0xF6, 0xBE, 0x25, 0xA4, 0x99]
state = [pt[i] ^ r1key[i] for i in range(0, 16)]
state = self.subbytes(state)
state = self.shiftrows(state)
state = self.mixcolumns(state)
return self.sbox(state[bnum] ^ key[bnum])
And we insert it into the system by modifying the analysis script in initAnalysis():
leakage_object = chipwhisperer.analyzer.attacks.models.AES128_8bit.AES128_8bit(Round2)
You can perform the same CPA attack, modified to occur around the second round. In this example I found points (20520, 21950) worked well - but you can try a much larger point-range, and then scale that down to get a faster calculation. This gives us the round-2 key, in this example appears to be AA 61 B3 E3 C7 AE 5F EB 1F 02 82 1D A1 27 26 84:

Using the key-schedule widget, you can then determine the true initial key was 94285d4d6dcfec08d8acddf6be25a499 (which matches what was programmed in this example):
Note in addition you can perform the operation 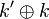 to recover
to recover 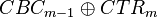 . If we knew either one of those we could then completely break AES-CCM, since we would know the AES-CBC I.V., along with the AES-CTR nonce/format.
. If we knew either one of those we could then completely break AES-CCM, since we would know the AES-CBC I.V., along with the AES-CTR nonce/format.
For a well-known implementation (say in IEEE 802.15.4) we are done, as the nonce format is known. You can perform an encryption with the known nonce to recover 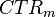 , then immediately recover
, then immediately recover 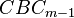 . Note this isn't the true I.V. as written in the file, but the result of the AES-CBC state up until the first encryption block was performed. Thus you cannot change the authentication-only blocks without doing further work to reverse back to the original I.V.
. Note this isn't the true I.V. as written in the file, but the result of the AES-CBC state up until the first encryption block was performed. Thus you cannot change the authentication-only blocks without doing further work to reverse back to the original I.V.
In the event the AES-CTR nonce input is unknown, additional work is required (detailed below).
Step #2: AES-CBC MAC Block #2
Repeating this for block #2 is exactly the same as before. Note you will need to perform a capture which triggers on the second block, which may require changes to the firmware source code.
Once you recover Block #1, you can calculate 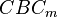 . Recovering block #2 means you could use
. Recovering block #2 means you could use 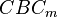 to determine
to determine 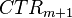 . Then you can decrypt
. Then you can decrypt 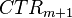 to determine the AES-CTR nonce format.
to determine the AES-CTR nonce format.
Example Bootloader
The example bootloader has a simplified AES-CCM implementation (NB: do NOT use this as a reference for a good implementation!). It accomplishes the basic goals only of having:
- Header data that is authenticated but not encrypted
- An encrypted MAC tag
- A bunch of encrypted firmware blocks
Each block sent to the bootloader is 19 bytes long. The first byte indicates the type - header, auth tag, or data. If a new 'header' message is received it will abort any ongoing processing of existing data and restart the bootloader process.
All messages share this feature:
- CRC-16: A 16-bit checksum using the CRC-CCITT polynomial (0x1021). The LSB of the CRC is sent first, followed by the MSB. The bootloader will reply over the serial port, describing whether or not this CRC check was valid.
Header Frame
-
0x01: 1 byte of fixed header - Header Info: 14 bytes of "header" data which could be version or other such stuff.
- Length: Number of encrypted data frames (NOT including the auth-tag frame) that will follow.
Note the 16 bytes of the header info + length are fed into the AES-CBC algorithm as part of the auth-tag generation. That is this data is authenticated but not encrypted.
+------+------+------+------+ .... +------+------+------+------+ | 0x01 | Header Info (14 bytes)| Length | CRC-16 | +------+------+------+------+ .... +------+------+------+------+
Auth Tag Frame
-
0x02: 1 byte of fixed header - Auth-Tag: The expected output of the AES-CBC algorithm after processing the authenticated only data + decrypted data frames. This is then encrypted in AES-CTR mode with the CTR set to 0.
|<----- Encrypted block (16 bytes) ------>|
| AES-CTR Encryption with CTR=0 |
| |
+------+------+------+------+ .... +------+------+------+------+
| 0x02 | Auth-Tag (encrypted MAC) | CRC-16 |
+------+------+------+------+ .... +------+------+------+------+
Data block frame
-
0x03: 1 byte of fixed header - Encrypted Data: Data encrypted in AES-CTR mode, with the CTR starting at 1 and incrementing.
|<----- Encrypted block (16 bytes) ------>|
| AES-CTR Encryption with CTR=1,2,3..N |
| |
+------+------+------+------+ .... +------+------+------+------+
| 0x03 | Data (16 Bytes) | CRC-16 |
+------+------+------+------+ .... +------+------+------+------+
The bootloader responds to each command with a single byte indicating if the CRC-16 was OK or not:
+------+
CRC-OK: | 0xA1 |
+------+
+------+
CRC Failed: | 0xA4 |
+------+
Once ALL messages are received, the bootloader will respond with a signature OK or not message:
+------+
Sig-OK: | 0xB1 |
+------+
+------+
Sig Failed: | 0xB4 |
+------+
Note details of the AES-CTR nonce, AES-CBC I.V., and key are stored in the firmware itself. In this example they are not downloaded as part of the encrypted firmware file.