| As of August 2020 the site you are on (wiki.newae.com) is deprecated, and content is now at rtfm.newae.com. |
Difference between revisions of "Attacking TEA with CPA"
(Created page with "= TEA Encryption = TEA (Tiny Encryption Algorithm) is a simple encryption algorithm that is meant to be simple enough to memorize. It uses a 128 bit key to encrypt 64 bits of...") |
(→TEA Encryption) |
||
| Line 14: | Line 14: | ||
</pre> | </pre> | ||
If you're used to looking at the AES algorithm, this one probably looks extremely simple. However, it is surprisingly secure. As of 2016, very few attacks on TEA are known - the best cryptanalysis results require <math>2^{121.5}</math> guesses against a shortened version of the algorithm! The only real weakness is that every key has three other equivalent keys - that is, there are four different keys that all give the exact same encrypted output. This is not a showstopper because <math>2^{126}</math> keys is still too many to brute-force. | If you're used to looking at the AES algorithm, this one probably looks extremely simple. However, it is surprisingly secure. As of 2016, very few attacks on TEA are known - the best cryptanalysis results require <math>2^{121.5}</math> guesses against a shortened version of the algorithm! The only real weakness is that every key has three other equivalent keys - that is, there are four different keys that all give the exact same encrypted output. This is not a showstopper because <math>2^{126}</math> keys is still too many to brute-force. | ||
| + | |||
| + | In order to complete a CPA attack, we need to find some sensitive points of the algorithm. Breaking up the first round of the one-liner | ||
| + | <pre> | ||
| + | v[0] += ((v[1]<<4) + k[0]) ^ (v[1] + sum) ^ ((v[1]>>5) + k[1]); | ||
| + | </pre> | ||
| + | gives | ||
| + | <pre> | ||
| + | uint32_t a = (v[1] << 4) + k[0]; // Attack point 1 | ||
| + | uint32_t b = v[1] + 0x9e3779b9; // | ||
| + | uint32_t c = (v[1] >> 5) + k[1]; // Attack point 2 | ||
| + | v[0] += (a ^ b ^ c); // Attack point 3 | ||
| + | </pre> | ||
| + | The three attack points here are good spots to attack because they are non-linear: addition can cause a single changed bit to carry through to several bits of the result. However, all three of these points have limitations. | ||
| + | # This expression includes a left-shift of 4 bits, so we have no control over the bottom 4 bits. This means we cannot use CPA to recover all 32 bits of <code>k[0]</code> - we can only get 28 of them. | ||
| + | # Similarly, this expression includes a right-shift of 5 bits, so we can only get at the bottom 27 bits. | ||
| + | # The last XOR combines the first two results, which use both words of the key (<code>k[0]</code> and <code>k[1]</code>). This means that we can only use it if we already know some of the bits in one of these keys (ie: we can only find the first byte of <code>k[0]</code> if we know the first byte of <code>k[1]</code>). | ||
| + | However, this is enough information to recover both of these words. Once we know these 64 bits, the second half of the key can be recovered in exactly the same way. | ||
Revision as of 12:23, 4 July 2016
TEA Encryption
TEA (Tiny Encryption Algorithm) is a simple encryption algorithm that is meant to be simple enough to memorize. It uses a 128 bit key to encrypt 64 bits of plaintext with the following C code:
void tea_encrypt(uint32_t* v, uint32_t* k)
{
uint32_t sum=0, i;
uint32_t delta= 0x9e3779b9;
for (i=0; i < 32; i++) {
sum += delta;
v[0] += ((v[1]<<4) + k[0]) ^ (v[1] + sum) ^ ((v[1]>>5) + k[1]);
v[1] += ((v[0]<<4) + k[2]) ^ (v[0] + sum) ^ ((v[0]>>5) + k[3]);
}
}
If you're used to looking at the AES algorithm, this one probably looks extremely simple. However, it is surprisingly secure. As of 2016, very few attacks on TEA are known - the best cryptanalysis results require 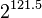 guesses against a shortened version of the algorithm! The only real weakness is that every key has three other equivalent keys - that is, there are four different keys that all give the exact same encrypted output. This is not a showstopper because
guesses against a shortened version of the algorithm! The only real weakness is that every key has three other equivalent keys - that is, there are four different keys that all give the exact same encrypted output. This is not a showstopper because 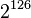 keys is still too many to brute-force.
keys is still too many to brute-force.
In order to complete a CPA attack, we need to find some sensitive points of the algorithm. Breaking up the first round of the one-liner
v[0] += ((v[1]<<4) + k[0]) ^ (v[1] + sum) ^ ((v[1]>>5) + k[1]);
gives
uint32_t a = (v[1] << 4) + k[0]; // Attack point 1 uint32_t b = v[1] + 0x9e3779b9; // uint32_t c = (v[1] >> 5) + k[1]; // Attack point 2 v[0] += (a ^ b ^ c); // Attack point 3
The three attack points here are good spots to attack because they are non-linear: addition can cause a single changed bit to carry through to several bits of the result. However, all three of these points have limitations.
- This expression includes a left-shift of 4 bits, so we have no control over the bottom 4 bits. This means we cannot use CPA to recover all 32 bits of
k[0]- we can only get 28 of them. - Similarly, this expression includes a right-shift of 5 bits, so we can only get at the bottom 27 bits.
- The last XOR combines the first two results, which use both words of the key (
k[0]andk[1]). This means that we can only use it if we already know some of the bits in one of these keys (ie: we can only find the first byte ofk[0]if we know the first byte ofk[1]).
However, this is enough information to recover both of these words. Once we know these 64 bits, the second half of the key can be recovered in exactly the same way.