Template Attacks

Template attacks are a powerful type of side-channel attack. These attacks are a subset of profiling attacks, where an attacker creates a "profile" of a sensitive device and applies this profile to quickly find a victim's secret key.

Template attacks require more setup than CPA attacks. To perform a template attack, the attacker must have access to another copy of the protected device that they can fully control. Then, they must perform a great deal of pre-processing to create the template - in practice, this may take dozens of thousands of power traces. However, the advantages are that template attacks require a very small number of traces from the victim to complete the attack. With enough pre-processing, the key may be able to be recovered from just a single trace.

There are four steps to a template attack:

1. Using a copy of the protected device, record a large number of power traces using many different inputs (plaintexts and keys). Ensure that enough traces are recorded to give us information about each subkey value.
2. Create a template of the device's operation. This template notes a few "points of interest" in the power traces and a multivariate distribution of the power traces at each point.
3. On the victim device, record a small number of power traces. Use multiple plaintexts. (We have no control over the secret key, which is fixed.)
4. Apply the template to the attack traces. For each subkey, track which value is most likely to be the correct subkey. Continue until the key has been recovered.

Signals, Noise, and Statistics

Before looking at the details of the template attack, it is important to understand the statistics concepts that are involved. A template is effectively a multivariate distribution that describes several key samples in the power traces. This section will describe what a multivariate distribution is and how it can be used in this context.

Noise Distributions

Electrical signals are inherently noisy. Any time we take a voltage measurement, we don't expect to see a perfect, constant level. For example, if we attached a multimeter to a 5 V source and took 4 measurements, we might expect to see a data set like (4.95, 5.01, 5.06, 4.98). One way of modelling this voltage source is

$\mathbf{X} = X_{actual} + \mathbf{N}$

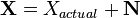
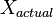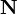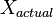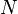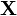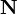where $X_{actual}$ is the noise-free level and $\mathbf{N}$ is the additional noise. In our example, $X_{actual}$ would be exactly 5 V. Then, $N$ is a random variable: every time we take a measurement, we can expect to see a different value. Note that $\mathbf{X}$ and $\mathbf{N}$ are bolded to show that they are random variables.

A simple model for these random variables uses a Gaussian distribution (read: a bell curve). The probability density function (PDF) of a Gaussian distribution is

$f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-(x - \mu)^2 / 2\sigma^2}$

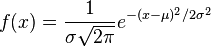
where 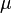$\mu$ is the mean and 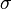$\sigma$ is the standard deviation. For instance, our voltage source might have a mean of 5 and a standard deviation of 0.5. We can use the PDF to calculate how likely a certain measurement is. Using this distribution,

$f(5.1) \approx 0.7821$

$f(7.0) \approx 0.0003$

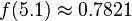
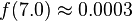
so we're very unlikely to see a reading of 7 V. We'll use this to our advantage in this attack: if 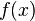$f(x)$ is very small for one of our subkey guesses, it's probably a wrong guess.

Multivariate Statistics

TODO: basics of multivariable stats

Profiling a Device

Points of Interest