Correlation Power Analysis
Correlation Power Analysis (CPA) is an attack that allows us to find a secret encryption key that is stored on a victim device. There are 4 steps to a CPA attack:
- Write down a model for the victim's power consumption. This model will look at one specific point in the encryption algorithm. (ie: after step 2 of the encryption process, the intermediate result is
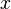 , so the power consumption is
, so the power consumption is 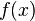 .)
.) - Get the victim to encrypt several different plaintexts. Record a trace of the victim's power consumption during each of these encryptions.
- Attack small parts (subkeys) of the secret key:
- Consider every possible option for the subkey. For each guess and each trace, use the known plaintext and the guessed subkey to calculate the power consumption according to our model.
- Calculate the Pearson correlation coefficient between the modeled and actual power consumption. Do this for every data point in the traces.
- Decide which subkey guess correlates best to the measured traces.
- Put together the best subkey guesses to obtain the full secret key.
This page discusses some of the basics of these steps, describing what models are typically used in CPA attacks and how the Pearson correlation coefficient is calculated.
Modeling Power Consumption
Electronic computers (microcontrollers, FPGAs, etc) have two components to their power consumption. First, static power consumption is the power required to keep the device running. This static power depends on things like the number of transistors inside the device. Secondly, and more importantly, dynamic power consumption depends on the data moving around inside the device. Every time a bit is changed from a 0 to a 1 (or vice versa), some current is required to (dis)charge the data lines. The dynamic power is the part that we're interested in - it can tell us what's happening inside.
One of the simplest models for power consumption is the Hamming Distance model. The Hamming Distance between two binary numbers is the number of different bits in the numbers. For example,
HammingDistance(00110000, 00100011) = 3
because there are 3 unequal bits in these two numbers. An easy way to calculate the Hamming Distance is
HammingDistance(x, y) = HammingWeight(x ^ y)
where ^ is the XOR operator, and the Hamming Weight is the number of 1s in a binary number. Using the example above,
HammingDistance(00110000, 00100011)
= HammingWeight(00010011)
= 3
because 00010011 has three bits set.
We can use the Hamming Distance model in our CPA attacks. If we can find a point in the encryption algorithm where the victim changes a variable from x to y, then we can estimate that the power consumption is proportional to Hamming Distance(x, y). Often, our model can even be a bit simpler: if we assume that the victim is replacing the value x = 0, then our power model is
l(y) = HammingWeight(y)
Calculating the Correlation Coefficient
Attacking the Subkeys
Example: AES-128
Here we will assume the attack has a power trace 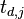 , where
, where 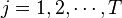 is the time index in the trace, and
is the time index in the trace, and 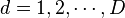 is the trace number. Thus the attacker makes
is the trace number. Thus the attacker makes 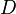 measurements, each one
measurements, each one 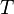 points long. If the attacker knew exactly where a cryptographic operation occurred, they would need to only measure a single point such that
points long. If the attacker knew exactly where a cryptographic operation occurred, they would need to only measure a single point such that 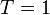 . For each trace
. For each trace 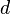 , the attacker also knows the plaintext or ciphertext corresponding to that power trace, defined as
, the attacker also knows the plaintext or ciphertext corresponding to that power trace, defined as 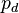 .
.
Assume also the attacker has a model of how the power consumption of the device depends on some intermediate value. For example the attacker could assume the power consumption of a microcontroller was dependent on the hamming weight of the intermediate value. We will define 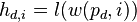 , where
, where 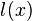 is the leakage model for a given intermediate value, and
is the leakage model for a given intermediate value, and 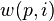 generates an intermediate value given the input plaintext and the guess number
generates an intermediate value given the input plaintext and the guess number 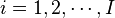 .
.
This intermediate value will be selected to depend on the input plaintext and a small portion of the secret key. For example with AES, each byte of the plaintext is XOR'd with each byte (subkey) of the secret key. In this example we would have:
This implies that the input plaintext 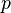 is being attacked a single byte at a time, which means we are attacking a single byte of the AES key at a time. While we still need to enumerate all possibilities for this subkey, we now only have
is being attacked a single byte at a time, which means we are attacking a single byte of the AES key at a time. While we still need to enumerate all possibilities for this subkey, we now only have 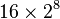 instead of
instead of 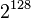 possibilities for AES-128.
possibilities for AES-128.
We will be next using the correlation coefficient to look for a linear relationship between the predicted power consumption 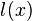 and the measured power consumption
and the measured power consumption 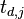 . For this reason it is desirable to have a non-linear relationship between
. For this reason it is desirable to have a non-linear relationship between 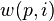 and either
and either 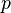 or
or 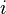 , as we will otherwise see a linear relationship for all values of
, as we will otherwise see a linear relationship for all values of 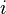 . In this case we take advantage of the non-linear substitution boxes (S-Boxes) in the algorithm, which are simply lookup tables which have been selected to have minimal possible correlation between the input and output. The emphasis on minimum possible correlation between input and output is a requirement to avoid certain linear cryptographic attacks.
. In this case we take advantage of the non-linear substitution boxes (S-Boxes) in the algorithm, which are simply lookup tables which have been selected to have minimal possible correlation between the input and output. The emphasis on minimum possible correlation between input and output is a requirement to avoid certain linear cryptographic attacks.
Finally, we can calculate the correlation coefficient for each point 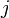 over all traces
over all traces 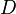 , for each of the possible subkey values
, for each of the possible subkey values 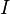 , as in the following:
, as in the following:
This is simply Pearson's correlation coefficient, given below, where 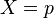 , and
, and 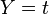 :
:
The problem of finding a known signal in a noisy measurement exists in many other fields beyond side-channel analysis. These two equations are referred to as the normalized cross-correlation, and frequently used in digital imaging for matching a known `template' to an image, e.g. finding the location of some specific item in a photo of a room.
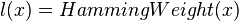
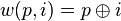
![{r_{i,j}} = \frac{{\sum\nolimits_{d = 1}^D {\left[ {\left( {{h_{d,i}} - \overline {{h_i}} } \right)\left( {{t_{d,j}} - \overline {{t_j}} } \right)} \right]} }}{{\sqrt {\sum\nolimits_{d = 1}^D {{{\left( {{h_{d,i}} - \overline {{h_i}} } \right)}^2}} \sum\nolimits_{d = 1}^D {{{\left( {{t_{d,j}} - \overline {{t_j}} } \right)}^2}} } }}](/images/math/4/3/e/x43ec93b3925401eb381eff776aef625e.png.pagespeed.ic.CDstywW1XH.png)
![{\rho _{X,Y}} = \frac{{{\mathop{\rm cov}} \left( {X,Y} \right)}}{{{\sigma _X}{\sigma _Y}}} = \frac{{E\left[ {\left( {X - {\mu _X}} \right)\left( {Y - {\mu _Y}} \right)} \right]}}{{\sqrt {E\left[ {{{\left( {X - {\mu _X}} \right)}^2}} \right]} \sqrt {E\left[ {{{\left( {Y - {\mu _Y}} \right)}^2}} \right]} }}](/images/math/a/7/6/xa76d678c1d581ff97b381cbd920fab35.png.pagespeed.ic.ViX1agfUlU.png)