TEA (Tiny Encryption Algorithm) is a simple encryption algorithm that is meant to be simple enough to memorize. It uses a 128 bit key to encrypt 64 bits of plaintext with the following C code:

void tea_encrypt(uint32_t* v, uint32_t* k)
{
    uint32_t sum=0, i;
    uint32_t delta= 0x9e3779b9;
    for (i=0; i < 32; i++) {
        sum  += delta;
        v[0] += ((v[1]<<4) + k[0]) ^ (v[1] + sum) ^ ((v[1]>>5) + k[1]);
        v[1] += ((v[0]<<4) + k[2]) ^ (v[0] + sum) ^ ((v[0]>>5) + k[3]);
    }
}

If you're used to looking at the AES algorithm, this one probably looks extremely simple. However, it is surprisingly secure. As of 2016, very few attacks on TEA are known - the best cryptanalysis results require 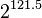guesses against a shortened version of the algorithm! The only real weakness is that every key has three other equivalent keys - that is, there are four different keys that all give the exact same encrypted output. This is not a showstopper because 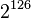keys is still too many to brute-force.

In order to complete a CPA attack, we need to find some sensitive points of the algorithm. Breaking up the first round of the one-liner

v[0] += ((v[1]<<4) + k[0]) ^ (v[1] + sum) ^ ((v[1]>>5) + k[1]);

gives

uint32_t a = (v[1] << 4) + k[0]; // Attack point 1
uint32_t b = v[1] + 0x9e3779b9;  //
uint32_t c = (v[1] >> 5) + k[1]; // Attack point 2
v[0] += (a ^ b ^ c);             // Attack point 3

The three attack points here are good spots to attack because they are non-linear: addition can cause a single changed bit to carry through to several bits of the result. However, all three of these points have limitations.

1. This expression includes a left-shift of 4 bits, so we have no control over the bottom 4 bits. This means we cannot use CPA to recover all 32 bits of k[0] - we can only get 28 of them.
2. Similarly, this expression includes a right-shift of 5 bits, so we can only get at the bottom 27 bits.
3. The last XOR combines the first two results, which use both words of the key (k[0] and k[1]). This means that we can only use it if we already know some of the bits in one of these keys (ie: we can only find the first byte of k[0] if we know the first byte of k[1]).

However, this is enough information to recover both of these words. Once we know these 64 bits, the second half of the key can be recovered in exactly the same way.