Difference between revisions of "Tutorial A8 32bit AES"

Latest revision as of 10:51, 1 May 2018

Most of our previous tutorials were running on 8-bit modes of operation. We can target typical implementation on ARM devices which actually looks a little different.

This tutorial is ONLY possible if you have an ARM target. For example the UFO Board with the STM32F3 target (or similar).

Background

A 32-bit machine can operate on 32-bit words, so it seems wasteful to use the same 8-bit operations. Indeed we can speed up the AES operation considerably by generating several tables (called T-Tables), as was described in the book The Design of Rijndael which was published by the authors of AES.

In order to take advantage of our 32 bit machine, we can examine a typical round of AES. With the exception of the final round, each round looks like:

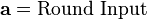
$\mathbf{a} = \text{Round Input}$

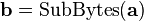
$\mathbf{b} = \text{SubBytes}(\mathbf{a})$

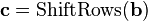
$\mathbf{c} = \text{ShiftRows}(\mathbf{b})$

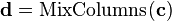
$\mathbf{d} = \text{MixColumns}(\mathbf{c})$

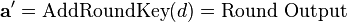
$\mathbf{a'} = \text{AddRoundKey}(d) = \text{Round Output}$

We'll leave AddRoundKey the way it is. The other operations are:

$b_{i,j} = \text{sbox}[a_{i,j}]$

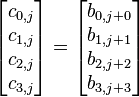
$\begin{bmatrix} c_{0,j} \\ c_{1,j} \\ c_{2,j} \\ c_{3,j} \end{bmatrix} = \begin{bmatrix} b_{0, j+0} \\ b_{1, j+1} \\ b_{2, j+2} \\ b_{3, j+3} \end{bmatrix}$

$\begin{bmatrix} d_{0,j} \\ d_{1,j} \\ d_{2,j} \\ d_{3,j} \end{bmatrix} = \begin{bmatrix} 02 & 03 & 01 & 01 \\ 01 & 02 & 03 & 01 \\ 01 & 01 & 02 & 03 \\ 03 & 01 & 01 & 02 \end{bmatrix} \times \begin{bmatrix} c_{0,j} \\ c_{1,j} \\ c_{2,j} \\ c_{3,j} \end{bmatrix}$

Note that the ShiftRows operation 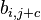$b_{i, j+c}$ is a cyclic shift and the matrix multiplcation in MixColumns denotes the xtime operation in GF( $2^8$ ).

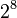It's possible to combine all three of these operations into a single line. We can write 4 bytes of 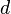$d$ as the linear combination of four different 4 byte vectors:

$\begin{bmatrix} d_{0,j} \\ d_{1,j} \\ d_{2,j} \\ d_{3,j} \end{bmatrix} = \begin{bmatrix} 02 \\ 01 \\ 01 \\ 03 \end{bmatrix} \text{sbox}[a_{0,j+0}]\ \oplus \begin{bmatrix} 03 \\ 02 \\ 01 \\ 01 \end{bmatrix} \text{sbox}[a_{1,j+1}]\ \oplus \begin{bmatrix} 01 \\ 03 \\ 02 \\ 01 \end{bmatrix} \text{sbox}[a_{2,j+2}]\ \oplus \begin{bmatrix} 01 \\ 01 \\ 03 \\ 02 \end{bmatrix} \text{sbox}[a_{3,j+3}]$

Now, for each of these four components, we can tabulate the outputs for every possible 8-bit input:

$T_0[a] = \begin{bmatrix} 02 \times \text{sbox}[a] \\ 01 \times \text{sbox}[a] \\ 01 \times \text{sbox}[a] \\ 03 \times \text{sbox}[a] \\ \end{bmatrix}$

$T_1[a] = \begin{bmatrix} 03 \times \text{sbox}[a] \\ 02 \times \text{sbox}[a] \\ 01 \times \text{sbox}[a] \\ 01 \times \text{sbox}[a] \\ \end{bmatrix}$

$T_2[a] = \begin{bmatrix} 01 \times \text{sbox}[a] \\ 03 \times \text{sbox}[a] \\ 02 \times \text{sbox}[a] \\ 01 \times \text{sbox}[a] \\ \end{bmatrix}$

$T_3[a] = \begin{bmatrix} 01 \times \text{sbox}[a] \\ 01 \times \text{sbox}[a] \\ 03 \times \text{sbox}[a] \\ 02 \times \text{sbox}[a] \\ \end{bmatrix}$

These tables have 2^8 different 32-bit entries, so together the tables take up 4 kB. Finally, we can quickly compute one round of AES by calculating

$\begin{bmatrix} d_{0,j} \\ d_{1,j} \\ d_{2,j} \\ d_{3,j} \end{bmatrix} = T_0[a_0,j+0] \oplus T_1[a_1,j+1] \oplus T_2[a_2,j+2] \oplus T_3[a_3,j+3]$

All together, with AddRoundKey at the end, a single round now takes 16 table lookups and 16 32-bit XOR operations. This arrangement is much more efficient than the traditional 8-bit implementation. There are a few more tradeoffs that can be made: for instance, the tables only differ by 8-bit shifts, so it's also possible to store only 1 kB of lookup tables at the expense of a few rotate operations.

Note that T-tables don't have a big effect on AES from a side-channel analysis perspective. The SubBytes output is still buried in the T-tables and the other operations are linear, so it's still possible to attack 32-bit AES using the same 8-bit attack methods.

Building Firmware

You will have to build with the PLATFORM set to one of the ARM targets (such as CW308_STM32F0 for the STM32F0 victim, or CW308_STM32F3 for the STM32F3 victim). If you haven't setup the ARM build environment see the page CW308T-STM32F#Example_Projects. Assuming your build environment is OK, you can build it as follows:

  cd chipwhisperer\hardware\victims\firmware\simpleserial-aes
  make PLATFORM=CW308_STM32F3 CRYPTO_TARGET=MBEDTLS

If this works you should get something like the following:

  Creating Symbol Table: simpleserial-aes-CW308_STM32F3.sym
  arm-none-eabi-nm -n simpleserial-aes-CW308_STM32F3.elf > simpleserial-aes-CW308_
  STM32F3.sym
  Size after:
     text    data     bss     dec     hex filename
     8440    1076   10320   19836    4d7c simpleserial-aes-CW308_STM32F3.elf
     +--------------------------------------------------------
     + Built for platform CW308T: STM32F3 Target
     +--------------------------------------------------------

Hardware Setup

Using a UFO board, connect your desired STM32Fx target:
Before finishing the hardware setup, you should connect to the target device. To do this you can use one of the standard setup scripts. This will provide a clock & setup TX/RX lines as expected for the STM32F, which is required for the programmer to work.

Programming STM32F Device

These instructions have been updated for ChipWhisperer 5. If you're using and earlier version, see https://wiki.newae.com/V4:CW308T-STM32F/ChipWhisperer_Bootloader

The STM32Fx devices have a built-in bootloader, and the ChipWhisperer software as of 3.5.2 includes support for this bootloader.

Important notes before we begin:

You MUST setup a clock and the serial lines for the chip. This is easily done by connecting to the scope and target, then running default_setup():

import chipwhisperer as cw
scope = cw.scope
target = cw.target(scope)
scope.default_setup()

On the STM32F1, you MUST adjust the clock frequency to 8MHz. The bootloader does not work with our usual 7.37 MHz clock frequency. This 8MHz frequency does not apply to the code that you're running on the device. Once you're done programming, you'll need to set the frequency back to F_CPU (likely 7.37MHz) For example:

scope.default_setup()
scope.clock.clkgen_freq = 8E6
#program target...
scope.clock.clkgen_freq = 7.37E6
#reset and run as usual

To access the bootloader you can perform these steps. They vary based on if you have a "Rev 02" board or a "Rev 03 or Later" board. The revision number is printed on the bottom side as part of the PCB part number (STM32F-03 is Rev -03 for example).

Rev -03 or Later

Run the following python code once you have the scope and target set up:

prog = cw.programmers.STM32FProgrammer
cw.program_target(scope, prog, "<path to fw hex file>")

If you get errors during the programming process:

Retry the programming process with a lower baud rate:

prog = cw.programmers.STM32FProgrammer
cw.program_target(scope, prog, "<path to fw hex file>", baud=38400)

If using a CW308 based STM, try mounting a jumper between the "SH-" and "SH+" pins at J16 (to the left of the SMA connector) on the UFO board. Retry programming with the jumper mounted.

Rev -02 Boards

The Rev -02 boards did not have all programming connections present. They require some additional steps:

Setup the device as usual:

scope = cw.scope()
target = cw.target(scope)
scope.default_setup()

Mount a jumper between the H1 and PDIC pins (again this is ONLY for the -02 rev).
Reset the ARM device either by pressing the reset button (newer UFO boards only), or by toggling power:
```
import time
scope.io.target_pwr = False
time.sleep(1)
scope.io.target_pwr = True
```

Program the device:

prog = cw.programmers.STM32FProgrammer
cw.program_target(scope, prog, "<path to fw hex file>")

The device should program, it may take a moment to fully program/verify on larger devices.
Remove the jumper between the H1/H2 pins.
Reset the ARM device either by pressing the reset button (newer UFO boards only), or by toggling power:
```
import time
scope.io.target_pwr = False
time.sleep(1)
scope.io.target_pwr = True
```

Capturing Traces

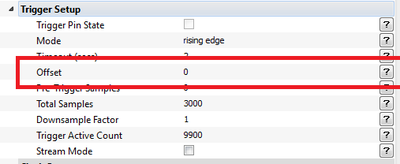
The capture process is similar to previous setups. After running the setup script, adjust the following settings:

Set the offset to by 0 samples:
Adjust the gain upward to get a good signal - note it will look VERY different from previous encryption examples:
Capture a larger (~500) number of traces.

Running Attack

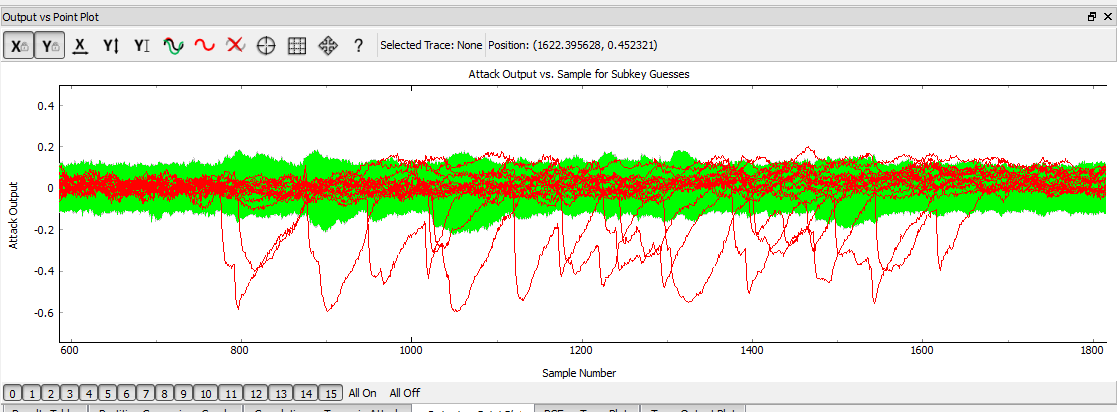
The attach is ran in the same manner as previous AES attacks, we use the same leakage assumptions as we don't actually care about the T-Table implementation. The resulting output vs. point location will look a little "messier", as shown here:

Links

Tutorials

See Tutorial Map for important information & suggested order of completion.

Theory

Correlation Power Analysis

Template Attacks

Extending AES-128 Attacks to AES-256

Basic Tutorials

Tutorial B1 Building a SimpleSerial Project

Tutorial B2 Viewing Instruction Power Differences

Tutorial B3-1 Timing Analysis with Power for Password Bypass

Tutorial B5 Breaking AES (Straightforward)

Tutorial B6 Breaking AES (Manual CPA Attack)

Tutorial B7 Profiling Attacks (with HW Assumption)

Tutorial B11 Breaking RSA

Advanced Tutorials

Tutorial A2 Introduction to Glitch Attacks (including Glitch Explorer)

Tutorial A3 VCC Glitch Attacks

Tutorial A5 Breaking AES-256 Bootloader

Tutorial A5-Bonus Breaking AES-256 Bootloader

Tutorial A7 Glitch Buffer Attacks

Tutorial A8 32bit AES

Hardware-Specific Tutorials

Tutorial P1 Stream Mode and Advanced Triggering (CW Pro)

Tutorial CW305-1 Building a Project

Tutorial CW305-2 Breaking AES on FPGA

Tutorial CW305-3 Clock Glitching

Tutorial CW305-4 Voltage Glitching with Crowbars

Archived Tutorials (v4/v3 only)

Tutorial B3-2 Timing Analysis with Power for Attacking TSB

Tutorial B4 Testing Two Partitions of Traces

Tutorial B5-2 Breaking DES (Straightforward)

Tutorial B8 Profiling Attacks (Manual Template Attack)

Tutorial B9 The Preprocessing Modules

Tutorial B10 Using with SASEBO-W CardOS or DPA Contest v4.2

Tutorial A1 Synchronization to Communication Lines

Tutorial A4 SAD Trigger for SCA and Glitch

Tutorial A6 Replication of Ilya Kizhvatov's XMEGA® Attack

Tutorial A9 Bypassing LPC1114 Read Protect

Difference between revisions of "Tutorial A8 32bit AES"

Latest revision as of 10:51, 1 May 2018

Contents

Background

Building Firmware

Hardware Setup

Programming STM32F Device

Rev -03 or Later

Rev -02 Boards

Capturing Traces

Running Attack

Links

Navigation menu

Personal tools

Namespaces

Variants

Views

More

Search

Navigation

Off-Wiki Links

Categories

Tools

@@ Line 6: / Line 6: @@
 A 32-bit machine can operate on 32-bit words, so it seems wasteful to use the same 8-bit operations. Indeed we can speed up the AES operation considerably by generating several tables (called T-Tables), as was described in the book [http://www.springer.com/gp/book/9783540425809 The Design of Rijndael] which was published by the authors of AES.
+In order to take advantage of our 32 bit machine, we can examine a typical round of AES. With the exception of the final round, each round looks like:
+<math>
+\mathbf{a} = \text{Round Input}
+</math>
+<math>
+\mathbf{b} = \text{SubBytes}(\mathbf{a})
+</math>
+<math>
+\mathbf{c} = \text{ShiftRows}(\mathbf{b})
+</math>
+<math>
+\mathbf{d} = \text{MixColumns}(\mathbf{c})
+</math>
+<math>
+\mathbf{a'} = \text{AddRoundKey}(d) = \text{Round Output}
+</math>
+We'll leave AddRoundKey the way it is. The other operations are:
+<math>
+b_{i,j} = \text{sbox}[a_{i,j}]
+</math>
+<math>
+\begin{bmatrix}
+c_{0,j}	\\
+c_{1,j}	\\
+c_{2,j}	\\
+c_{3,j}
+\end{bmatrix}
+=
+\begin{bmatrix}
+b_{0, j+0} \\
+b_{1, j+1} \\
+b_{2, j+2} \\
+b_{3, j+3}
+\end{bmatrix}
+</math>
+<math>
+\begin{bmatrix}
+d_{0,j}	\\
+d_{1,j}	\\
+d_{2,j}	\\
+d_{3,j}
+\end{bmatrix}
+=
+\begin{bmatrix}
+& 03 & 01 & 01 \\
+& 02 & 03 & 01 \\
+& 01 & 02 & 03 \\
+& 01 & 01 & 02
+\end{bmatrix}
+\times
+\begin{bmatrix}
+c_{0,j}	\\
+c_{1,j}	\\
+c_{2,j}	\\
+c_{3,j}
+\end{bmatrix}
+</math>
+Note that the ShiftRows operation <math>b_{i, j+c}</math> is a cyclic shift and the matrix multiplcation in MixColumns denotes the xtime operation in GF(<math>2^8</math>).
+It's possible to combine all three of these operations into a single line. We can write 4 bytes of <math>d</math> as the linear combination of four different 4 byte vectors:
+<math>
+\begin{bmatrix}
+d_{0,j}	\\
+d_{1,j}	\\
+d_{2,j}	\\
+d_{3,j}
+\end{bmatrix}
+=
+\begin{bmatrix}
+\\
+\\
+\\
+\end{bmatrix}
+\text{sbox}[a_{0,j+0}]\
+\oplus
+\begin{bmatrix}
+\\
+\\
+\\
+\end{bmatrix}
+\text{sbox}[a_{1,j+1}]\
+\oplus
+\begin{bmatrix}
+\\
+\\
+\\
+\end{bmatrix}
+\text{sbox}[a_{2,j+2}]\
+\oplus
+\begin{bmatrix}
+\\
+\\
+\\
+\end{bmatrix}
+\text{sbox}[a_{3,j+3}]
+</math>
+Now, for each of these four components, we can tabulate the outputs for every possible 8-bit input:
+<math>
+T_0[a] =
+\begin{bmatrix}
+\times \text{sbox}[a] \\
+\times \text{sbox}[a] \\
+\times \text{sbox}[a] \\
+\times \text{sbox}[a] \\
+\end{bmatrix}
+</math>
+<math>
+T_1[a] =
+\begin{bmatrix}
+\times \text{sbox}[a] \\
+\times \text{sbox}[a] \\
+\times \text{sbox}[a] \\
+\times \text{sbox}[a] \\
+\end{bmatrix}
+</math>
+<math>
+T_2[a] =
+\begin{bmatrix}
+\times \text{sbox}[a] \\
+\times \text{sbox}[a] \\
+\times \text{sbox}[a] \\
+\times \text{sbox}[a] \\
+\end{bmatrix}
+</math>
+<math>
+T_3[a] =
+\begin{bmatrix}
+\times \text{sbox}[a] \\
+\times \text{sbox}[a] \\
+\times \text{sbox}[a] \\
+\times \text{sbox}[a] \\
+\end{bmatrix}
+</math>
+These tables have 2^8 different 32-bit entries, so together the tables take up 4 kB. Finally, we can quickly compute one round of AES by calculating
+<math>
+\begin{bmatrix}
+d_{0,j}	\\
+d_{1,j}	\\
+d_{2,j}	\\
+d_{3,j}
+\end{bmatrix}
+=
+T_0[a_0,j+0] \oplus
+T_1[a_1,j+1] \oplus
+T_2[a_2,j+2] \oplus
+T_3[a_3,j+3]
+</math>
+All together, with AddRoundKey at the end, a single round now takes 16 table lookups and 16 32-bit XOR operations. This arrangement is much more efficient than the traditional 8-bit implementation. There are a few more tradeoffs that can be made: for instance, the tables only differ by 8-bit shifts, so it's also possible to store only 1 kB of lookup tables at the expense of a few rotate operations.
+Note that T-tables don't have a big effect on AES from a side-channel analysis perspective. The SubBytes output is still buried in the T-tables and the other operations are linear, so it's still possible to attack 32-bit AES using the same 8-bit attack methods.
 == Building Firmware ==
@@ Line 53: / Line 233: @@
 [[File:A8_outputvspoint.png]]
+== Links ==
 {{Template:Tutorials}}
 [[Category:Tutorials]]